Infiltration Models
Any mention of trade names, manufacturers or products does not imply an endorsement by the US Government of the United States Environmental Protection Agency. EPA and its employees do not endorse any commercial products, services, or enterprises.
Infiltration models presented on this web site were developed using Mathcad Plus 6.0 . Mathcad is a registered trademark of Mathsoft, Inc., of Cambridge, Massachusetts. The worksheets have been tested and found to be compatible with MathCad 7.0. To use the models, you will need to have your browser recognize and launch the MathCad application; or you can save the worksheet to a local storage media by right clicking on the link and selecting “Save Link As” or “Save Target As” and opening it at a later time.
When using the worksheets, parameter values can be easily changed and the resulting output can be quickly observed to evaluate any resulting changes. By using the tiling feature available within MathCad, the same worksheet can be loaded several times to allow comparisons of results for various model scenarios. Any changes made and saved to the same file name will result in the original information being lost. Therefore, it is recommended that a copy of the original files be archived for future use.
Phenomena of Water Infiltration in the Unsaturated Zone
Water applied to the soil surface through rainfall and irrigation events subsequently enters the soil through the process of infiltration. If the supply rate of water to the soil surface is greater than the soil's ability to allow the water to enter, excess water will either accumulate on the soil's surface or become runoff. Infiltrability is a term generally used in the disciplines of soil physics and hydrology to define the maximum rate at which rain or irrigation water can be absorbed by a soil under a given condition. Indirectly, infiltrability determines how much of the water will flow over the ground surface (i.e., runoff or overland flow), terminating in lakes, streams, or rivers, and how much will enter the soil. This term can be used in the estimation of water available for downward percolation through drainage, runoff, or returned to the atmosphere by the process of evapotranspiration.
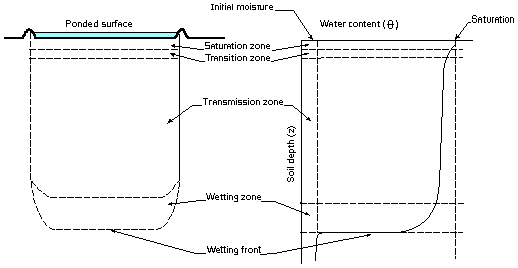
In this idealized profile for soil water distribution for a homogeneous soil, five zones are illustrated for the infiltration process.
- Saturated Zone - The pore space in this zone is filled with water or saturated. Depending on the length of time elapsed from the initial application of the water, this zone will generally extend only to a depth of a few millimeters.
- Transition Zone – This zone is characterized by a rapid decrease in water content with depth and will extend approximately a few centimeters.
- Transmission Zone – This zone is characterized by a small change in water content with depth. In general, the transmission zone is a lengthening unsaturated zone with uniform water content. The hydraulic gradient in this zone is primarily driven by gravitational forces.
- Wetting Zone – In this zone, the water content sharply decreases with depth from the water content of the transmission zone to near the initial water content of the soil.
- Wetting Front – This zone is characterized by a steep hydraulic gradient and forms a sharp boundary between the wet and dry soil. The hydraulic gradient is characterized primarily by metric potentials.
Beyond the wetting front, there is no visible penetration of water. Comprehensive reviews of the principles governing the infiltration process have been published by Philip (1969) and Hillel (1982).
Soil water infiltration is controlled by the rate and duration of water application, soil physical properties, slope, vegetation, and surface roughness. Generally, whenever water is ponded over the soil surface, the rate of infiltration exceeds the soil infiltrability. On the other hand, if water is applied slowly, the infiltration rate may be smaller than the soil infiltrability and the supply rate becomes a determining factor for the infiltration rate. This type of infiltration process is termed “supply controlled” (Hillel 1982). However, once the infiltration rate exceeds the soil infiltrability, it is the latter that determines the actual infiltration rate and thus the process becomes “profile controlled.”
Infiltration Models
SCS Model
The SCS model is an empirically developed approach to the water infiltration process (Jury, et al. 1991). It has been developed by first finding a mathematical function whose shape as a function of time matches the observed features of the infiltration rate. This function is then provided a physical explanation of the process. In semi-empirical models, most physical processes are represented by commonly accepted and simplistic conceptual methods rather than by equations derived from fundamentally physical principles. The commonly used semi-empirical infiltration model in the fields of soil physics and hydrology is the SCS model. A scenario was chosen to simulate water infiltration into a soil for conditions with rainfall and surface runoff by using the SCS model. Input parameters and simulation results are discussed in Estimation of Infiltration Rate in the Vadose Zone: Compilation of Simple Mathematical Models, Volume II. SCS MathCad Code (zip)
Philip's Two-Term Model
The Philip's Two-Term model (PHILIP2T) is a truncated power series solution developed by Philips (1957). During the initial stages of infiltration (when t is very small), the first term of the model/equation dominates the process. In this stage, the vertical infiltration proceeds at almost the same rate as absorption or horizontal infiltration. In this stage of infiltration, the gravity component, represented by the second term of the model/equation, is negligible. As infiltration continues, the second term becomes progressively more important until it dominates the infiltration process. Philips (1957) suggested the use of the two-term model in applied hydrology when t is not too large. A scenario was chosen to simulate the water infiltration into a sandy soil by using the PHILIP2T model. Input parameters and simulation results are discussed in Estimation of Infiltration Rate in the Vadose Zone: Compilation of Simple Mathematical Models, Volume II. Philip's Two-Term MathCad Code (zip)
Layered Green Ampt Model
The Green Ampt model has been modified in this application to calculate water infiltration into non-uniform soils by several researchers (Bouwer 1969, Fok 1970, Moore 1981, Ahuja and Ross 1983). The implementation for layered systems (GALAYER) used for this project was developed by Flerchinger, et al. (1989). Specifically, the model could be used for the determination of water infiltration over time in vertically heterogeneous soils. Two simulation scenarios were selected for inclusion in the applications worksheet. The first scenario was to estimate water infiltration into a soil with two layers (sand over a loam). The second scenario was designed to estimate the water infiltration into a soil with three layers (sand over loam, over clay). Comparisons and results are presented and discussed in Estimation of Infiltration Rate in the Vadose Zone: Compilation of Simple Mathematical Models, Volume II. Layered Green Ampt MathCad Code (zip)
Explicit Green Ampt Model
The initial Green Ampt model was the first physically based model/equation describing the infiltration of water into soil. It has been the subject of considerable development in soil physics and hydrology, owing to its simplicity and satisfactory performance for a great variety of water infiltration problems. This model yields cumulative infiltration and the infiltration rate as an implicit function of time (i.e., given a value of time (t), values of the cumulative infiltration (I) and the infiltration rate (q) can be directly obtained. Thus, the model functions are q(t) and I(t), rather than of t(q) and t(I).) The Explicit Green-Ampt model as defined and used for this project's application was developed by Salvucci and Entekhabi (1994). The application provides a straightforward and accurate estimation of infiltration for any given time. This formulation supposedly yields an error of less than 2 percent at all times when compared to the exact values resulting from the Implicit Green Ampt model. Explicit Green Ampt MathCad Code (zip)
Constant Flux Green Ampt Model
For the constant flux Green-Ampt model, two formulations are required: one for the condition that the application rate (r) is less than the saturated hydraulic conductivity (Ks), and one for the condition that the application rate is greater than the saturated hydraulic conductivity. When r<Ks, the infiltration rate (q) is always equal to the surface application rate (r) and the surface never becomes saturated. When r>Ks , the surface becomes saturated at the time of the initial application (t0). Constant Flux Green Ampt MathCad Code (zip)
Infiltration/Exfiltration Model
The vertical movement of water in the soil profile from the surface to water table is a dynamic condition. It can be conceptualized as being composed of basically two predominant processes: infiltration and exfiltration. Exfiltration can be envisioned as the processes dominating during drying periods; water released during this period can be thought of as being released through evaporation to the atmosphere. The model (INFEXF) selected for this project is a formulation of the Philips model developed by Eagleson (1978) to account for water infiltration during the wetting season and exfiltration during the drying season. Infiltration and exfiltration as described in this application assumes the soil medium to be effectively semi-infinite and the internal soil water content at the beginning of each storm event and inter-storm period is assumed to be uniform at its long-term and space-time average. The exfiltration equation is modified for the presence of natural vegetation through the approximate introduction of a distributed sink representing the moisture extraction by plant roots. Two scenarios are presented in the accompanying worksheet applications: water infiltration during the rainy season and water exfiltration during the drying season. Infiltration/Exfiltration MathCad Code (zip)
Complete Report
Estimation of Infiltration Rate in the Vadose Zone: Compilation of Simple Mathematical Models (EPA/600/R-97/128) February 1998
- Volume I (PDF) (84 pp, 412 K, About PDF)
- Volume II (PDF) (117 pp, 2.63 MB, About PDF)
