Basic Analyses

Additional Information on Classification and Regression Tree (CART) Analysis

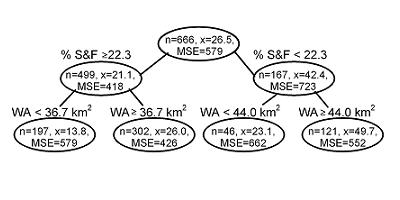
Classification and regression tree (CART) analysis recursively partitions observations in a matched data set, consisting of a categorical (for classification trees) or continuous (for regression trees) dependent (response) variable and one or more independent (explanatory) variables, into progressively smaller groups (De’ath and Fabricius 2000, Prasad et al. 2006).  Each partition is a binary split. During each recursion, splits for each explanatory variable are examined and the split that maximizes the homogeneity of the two resulting groups with respect to the dependent variable is chosen. A typical output from these analyses is shown below (in Figure 1).

Using CART Analysis in Causal Analysis

CART analysis is used in data exploration to classify systems that differ due to natural causes. CART analysis may be used to determine the relative importance of different variables for identifying homogeneous groups within the data set.

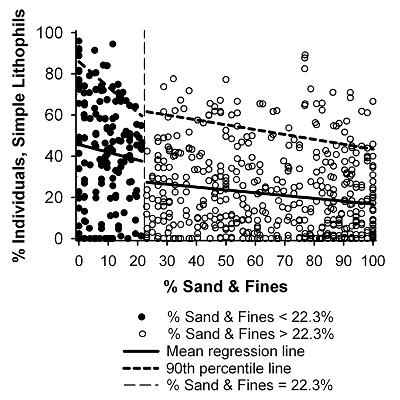
In Figure 1, the CART analysis results suggest that the relationship between the relative abundance of lithophilous fish and % sand and fines depends on watershed area. Based on this finding, one might consider classifying these sites based on drainage area into sites greater than or less than about 40 km².

CART analyses also might be used to help identify variables that may confound estimates of stressor-response relationships.

CART analysis also can help describe stressor-response relationships by identifying the levels of the stressor at which its functional relationship with the biological response might change. This application may be used to help identify inflection points or nonlinearities in a stressor-response relationship (Brenden et al. 2008). Apparent change points then can be investigated using other techniques (e.g., regression analysis) to determine whether they represent thresholds or other change points in the stressor-response relationship. For example, the previous CART analysis (in Figure 1) identified a split in the data set at % sand and fines = 22.3%. Regression analyses demonstrate that two groups are best described by different models: the y intercepts of the mean regression line and both the intercept and slope of the 90th-percentile line decreased for sites where the percentage of sand and fines exceeded 22.3% (in Figure 2). After the model is derived, it would be interpreted in the same way as the results from regression or quantile regression analyses.

Assumptions in Classification and Regression Tree Analysis (CART)

Unlike linear regression techniques, CART analysis does not assume a particular form of relationship between the independent and dependent variables. Therefore, CART can often be used even in cases where data are not suitable for analysis by linear regression. The objective of CART analysis is to create a decision tree that predicts the characteristics of the population of sites being studied. Therefore, the more sites (i.e., examples or observations) presented to the algorithm, the more accurately it will predict the characteristics of the population.

Simplification or “Pruning” of Classification and Regression Trees

Theoretically, CART algorithms could continue to split a data set until there are groups or nodes containing every observation in the data set.  In causal analysis, one is generally most interested in the first few splits of a data set.  Moreover, to avoid such overfitting of the data, algorithms used in CART generally simplify or “prune” the tree that contains all possible splits of the data to an optimal tree that contains a sufficient number of splits to describe the data.

Many algorithms use stopping criteria that may set the minimum number of observations needed in a group or node in order to split that group, the minimum number of observations needed in a terminal group or node in order to retain that group, or the minimum decrease in the overall lack of fit (i.e., usually the mean squared error) needed for a split of a group or node in order to retain that split.  These stopping criteria usually have default values, but they can be set by the user.  As some of these criteria are based on the number of observations in a group or node, the number of splits will be dependent on the total number of observations in a data set.

Other options for pruning trees include the use of cross-validation, where the CART analysis is conducted iteratively on random subsets of the data set, or validation of the resulting tree against a second, independent data set.  As a result, finding a final tree is a balance between model fit and the size of the data set available for analysis.