Basic Analyses
Tests of Significant Difference
Tests of significant differences most commonly test whether the difference between two mean values is significantly different from zero (Snedecor and Cochran 1989). However, in causal assessment, a more common question is whether an observation at a test site deviates significantly from the range of conditions observed at a reference site. For example, we may wish to compare total phosphorus concentrations (TP) at a biologically-degraded test site with TP at one similar reference site with unimpaired biota to establish whether elevated TP co-occurs with the observed biological degradation (see page on spatial co-occurrence).
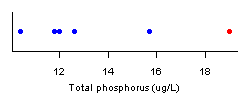
Non-Parametric Approaches
A simple approach for estimating the probability of observing a particular value relative to a set of reference observations is to note that the reference observations define a range of possibilities. That is, nitrogen (N) random reference observations at a site divide the range of possible values into N +1 intervals. Therefore, the probability that a subsequent observation is higher than the highest reference value is 1/(N +1). In the example described above, the probability of observing any observation greater than 16 is 1/(5+1), or 17%. More samples at the reference site would increase our ability to assert whether the observation at the test site could come from the reference site (i.e., that the test site is similar to the reference site).
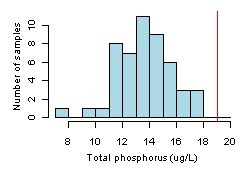
Parametric Approaches
Parametric estimates of prediction intervals can provide more informative comparisons than non-parametric techniques, but they require larger sample sizes, and they require that we assume that the observed values are drawn from a particular statistical distribution (e.g., a normal distribution). TP values shown (in Figure 2) appear to be normally distributed, and we calculate the sample mean value (Xmean ) as 13.6 and standard deviation (S) as 2.05. A quantile-quantile plot (not shown) confirms that values are nearly normally distributed. We can estimate the 95th percentile of the distribution using the following formula:
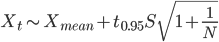
where Xt is the threshold associated with the 95th percentile of the distribution and t0.95 is the t-statistic for the 95th percentile with 50 degrees of freedom. In this example, the threshold is estimated as 17 µg/L, and our test site with TP = 19 µg/L is declared to be different from the reference distribution.
More Information
The discussion here has focused on comparing a single test site measurement with a set of samples collected at different times from a single reference site. The same types of tests could also be applied to a set of samples collected from multiple reference sites, if we were confident that the natural expectations at all of the references sites were identical. In practice, different streams are likely to vary in terms of natural expectations, and test site comparisons should take these natural variations into account. Quantile regression and prediction intervals from linear regression extend these ideas to situations in which one needs to control for the influence of one or more covarying factors.
The number of samples available at the reference site often limits our ability to determine whether a test site differs from reference expectations. In cases in which the number of reference samples is low (e.g., < 5), pooling samples from other sites to estimate a within-site standard deviation may be necessary.
Statistical methods to explicitly formulate the null hypothesis in terms of a range of possible values are available and discussed in Kilgour et al. (1998).
Regression Analysis
- How do I Run a Regression Analysis?
- What do Regression Results Mean?
- How do I Use Regression Analysis in Causal Analysis?
- More Information
Linear regression is an approach for quantifying the relationship between a dependent (response) variable and one or more independent (explanatory) variables. The relationship is often assumed to be a straight line, but may also be curvilinear or nonlinear.
How do I Run a Regression Analysis?
A regression tool is available in CADStat. Linear regression tools are also available in most spreadsheets and statistical programs.
What do Regression Results Mean?
After running a linear regression, most programs will provide statistics that describe the characteristics of the estimated fit to the data. These statistics include estimated values for the coefficients, the standard errors and p-values for those coefficients, and a measure of the degree the model accounted for observed variability in the response relative to a constant, null model (R2). Several existing resources provide complete explanations for these different statistics.
How do I Use Regression Analysis in Causal Analysis?
- Controlling for Natural Variability
- Propensity Score Analysis
- Predicting Environmental Conditions from Biological Observations (PECBO)
Linear regression is also a key technique for describing stressor-response relationships.
Quantile Regression
- How do I Run a Quantile Regression Analysis?
- What do Quantile Regression Results Mean?
- How do I Use Quantile Regression in Causal Analysis?
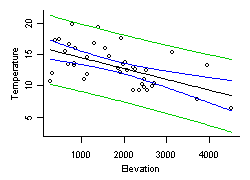
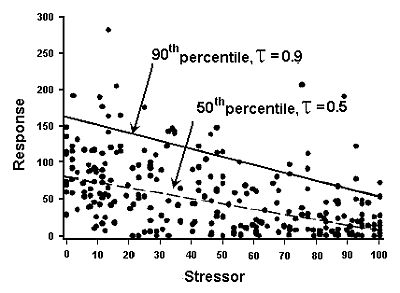
Quantile regression models the relationship between a specified conditional quantile (or percentile) of a dependent (response) variable and one or more independent (explanatory) variables (Cade and Noon 2003). As with mean regression, the relationship is often assumed to be a straight line (in Figure 4).
How do I Run a Quantile Regression Analysis?
What do Quantile Regression Results Mean?
How do I Use Quantile Regression in Causal Analysis?
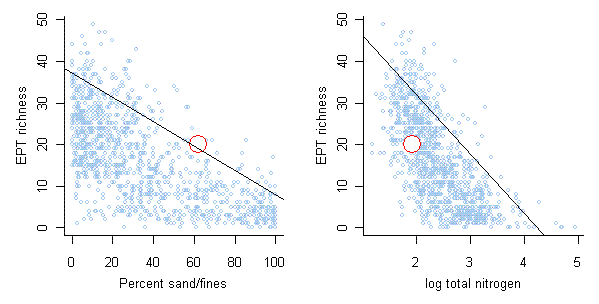
Quantile regression can be used to help describe stressor-response relationships. Quantile regression provides a means of estimating the location of the upper boundary of a scatter plot (e.g., the 90th percentile line in Figure 4). An assumption for using this upper boundary is that the wedge shape often observed in scatter plots of biological metrics results from the effects of other stressors co-occurring with the modeled stressor that cause additional negative effects on the biological response.
Classification and Regression Tree (CART) Analysis
- How do I Run a CART Analysis?
- What do CART Results Mean?
- How do I Use CART Analysis in Causal Analysis?
- More information
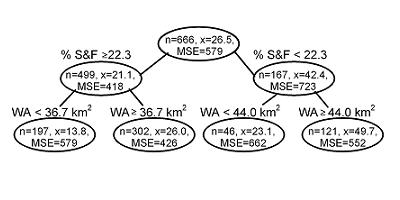
Classification and regression tree CART analysis recursively partitions observations in matched data set, consisting of a categorical (for classification trees) or continuous (for regression trees) dependent (response) variable and one or more independent (explanatory) variables, into progressively smaller groups (De'ath and Fabricius 2000, Prasad et al. 2006). Each partition is a binary split based on a single independent variable. A typical output from these analyses is shown below (in Figure 6).
How do I Run a CART Analysis?
What do CART Results Mean?
CART analysis constructs a set of decision rules that identify homogeneous groups of the response variable as a function of a set of explanatory variables (in Figure 1). During each recursion, splits for each explanatory variable are examined, and the split that maximizes the homogeneity of the two resulting groups with respect to the dependent variable is chosen. To avoid overfitting of the data, algorithms used in CART usually simplify or “prune” the tree that contains all possible splits of the data to an optimal tree that contains a sufficient number of splits to describe the data. For more background and details, see Additional Information on Classification and Regression Trees in the Helpful Links box.
How do I Use CART Analysis in Causal Analysis?
In general, CART analysis can be applied effectively to the causal analysis in three ways. When controlling for natural variability, CART analysis can be used in data exploration to classify systems that differ as a result of natural factors and to develop models that predict environmental conditions as a function of natural factors.
References
- Brenden TO, Wang L, Su Z (2008) Quantitative identification of disturbance thresholds in support of aquatic resource management. Environmental Management 42:821-832.
- Cade BS, Noon BR (2003) A gentle introduction to quantile regression for ecologists. Frontiers in Ecology and the Environment 1:412-420.
- Chaudhuri P, Loh WY (2002) Nonparametric estimation of conditional quantiles using quantile regression trees. Bernoulli 8:561-576.
- De'ath G, Fabricius KE (2000) Classification and regression trees: a powerful yet simple technique for ecological data analysis. Ecology 81(11):3178-3192.
- Kilgour BW, Somers KM, Matthews DE (1998) Using the normal range as a criterion for ecological significance in environmental monitoring and assessment. Ecoscience 5:542-550.
- Loh WY (2002) Regression trees with unbiased variable selection and interaction detection. Statistica Sinica 12:361-386.
- Prasad AM, Iverson LR, Liaw A (2006) Random forests for modeling the distribution of tree abundances. Ecosystems 9:181-199.
- Snedecor GW, Cochran WG (1989) Statistical Methods. Iowa State University Press, Ames IA.
Volume 4: Authors
